Kombinationen bei 2 Würfeln berechnen – Anleitung

In diesem Ratgeber erfahren Sie, wie Sie die Wahrscheinlichkeiten von Würfeln berechnen können. Der Schwerpunkt hierbei liegt dabei, dass Sie am Ende wissen, wie die Wahrscheinlichkeit berechnet wird, wie man dabei vorgeht und welche Ergebnisse möglich sind.

Der Würfel

Kniffel, Pasch und Mensch, ärgere dich nicht, das sind nur paar Beispiele wo Würfel eine Rolle in unserem Leben spielen. Der normale Würfel hat sechs Seiten, die jeweils von 1 bis 6 durchnummeriert sind. In diesem Ratgeber gehen wir davon aus, dass es sich um einen normalen, sechsseitigen Würfel handelt, der nicht manipuliert worden ist.

Wahrscheinlichkeiten bei einem Würfel

Bevor wir anfangen, über zwei Würfel zu sprechen und diese zu berechnen, sollten wir mit nur einem Würfel beginnen. Bei der Wahrscheinlichkeitsberechnung muss man immer zwei Werte ermitteln:

• Die Anzahl der günstigen Ereignisse.
• Die Anzahl der möglichen Ereignisse.

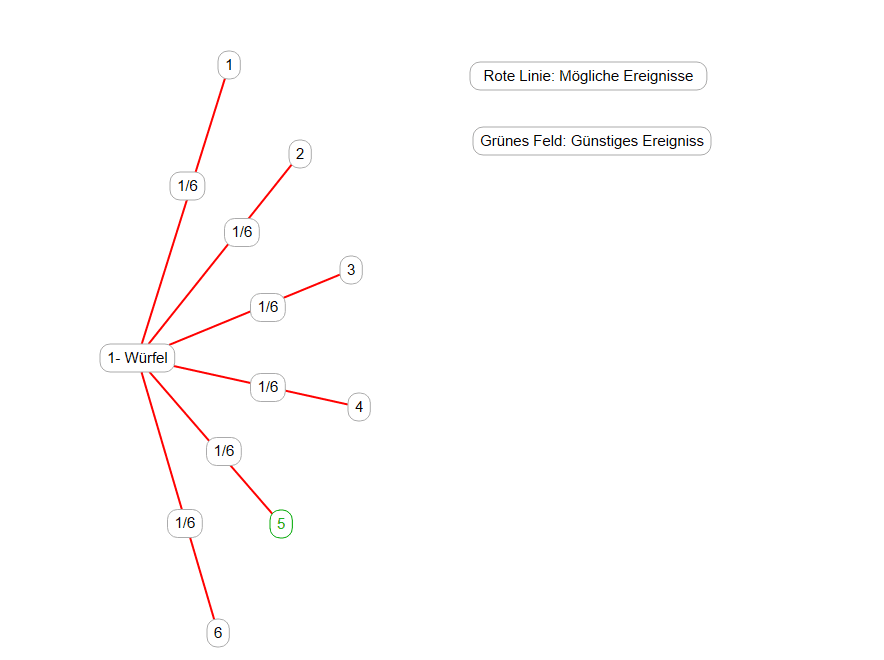
Wie viele Ausgangsmöglichkeiten gibt es beim Würfeln?

Gewürfelt werden können folgende Zahlen: 1, 2, 3, 4, 5, und 6. Diese Ereignisse sind möglich. Also insgesamt 6 mögliche Ereignisse.

Beispielaufgabe 1

Mal angenommen, wir wollen wissen, wie hoch die Wahrscheinlichkeit ist, eine 5 zu würfeln. Wie viele günstige Ereignisse gibt es dann? Richtig, nur eins, die 5.

Die Formel zur Berechnung der Wahrscheinlichkeit lautet:

P (E) = Anzahl günstiger Ergebnisse / Anzahl möglicher Ergebnisse

In unserem Fall also: P (E) = 1/6

Oder in Worten: Eins zu sechs

Beispielaufgabe 2

Wie hoch ist die Wahrscheinlichkeit eine gerade Zahl zu würfeln?
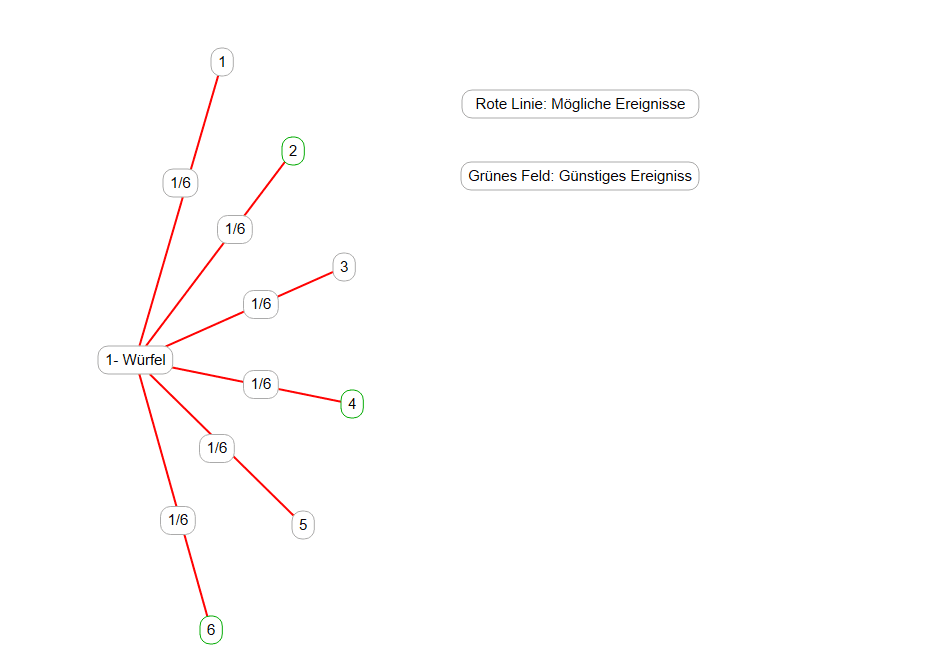
Wie viele gerade Zahlen hat ein Würfel? Richtig, es sind drei gerade Zahlen, und zwar: 2, 4 und 6. Also:

P(E) = 3/6 (drei zu sechs oder 50%)

Wahrscheinlichkeiten bei zwei Würfeln

Nun beginnen wir damit, die Wahrscheinlichkeit von zwei Würfeln zu berechnen. Der zweite Würfel hat exakt die gleichen Bedingungen wie der erste Würfel, auch die Anzahl der möglichen Ereignisse ändert sich nicht.
Beim Berechnen von zwei Würfeln bleibt die Berechnung ähnlich, wie bei einem Würfel. Das Einzige, was hinzukommt, ist die Multiplikation und die Addition.

Fangen wir mit einem Beispiel an:

Beispielaufgabe 3

Wie hoch ist die Wahrscheinlichkeit zweimal eine 4 zu würfeln?

Erster Wurf: Chance beträgt 1/6
Zweiter Wurf: Chance beträgt 1/6

P (E) = 1/6 * 1/6
P (E) = 1/36

Oder in Worten: 1 zu 36

Erklärung:

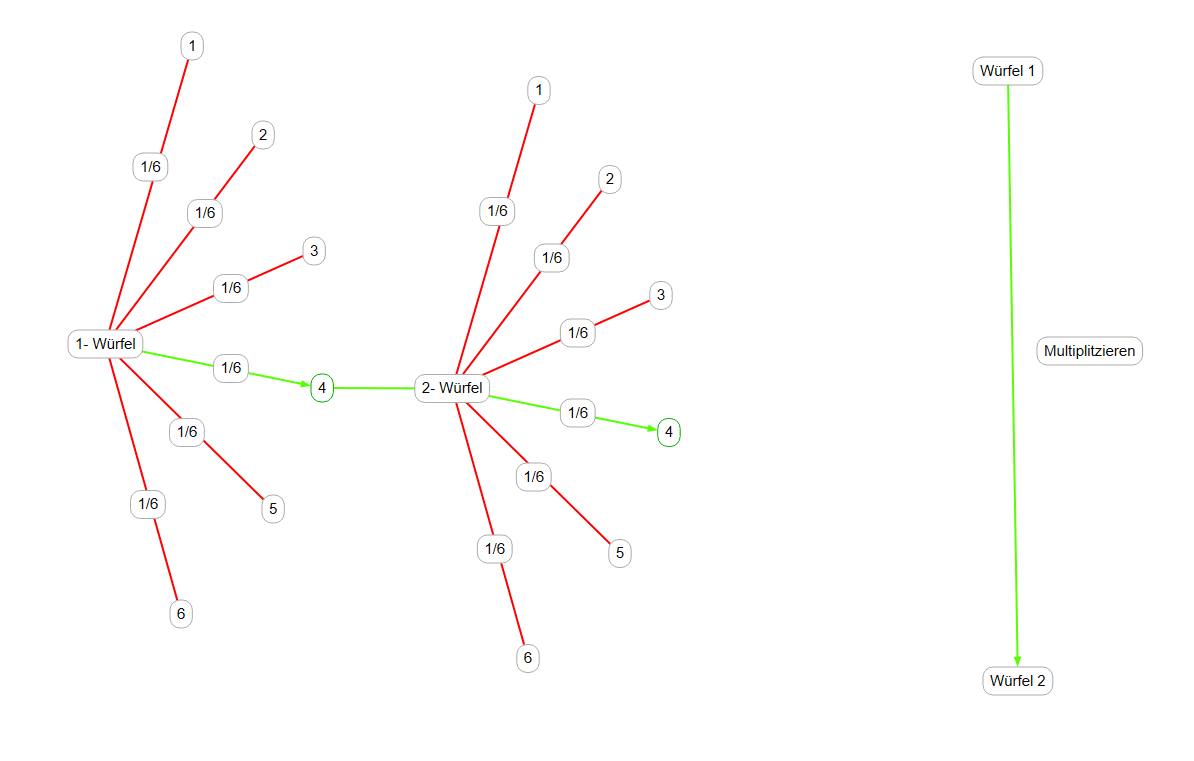
Wenn man sich einen Wahrscheinlichkeits-Stammbaum angucken würde und mit dieser Aufgabe vergleichen würde, dann würde man Folgendes feststellen:

Bewegt man sich im Stammbaum von Links nach Rechts, so werden die Brüche miteinander multipliziert.

Beispielaufgabe 4

Wie hoch ist die Wahrscheinlichkeit eine 3 und eine 5 zu würfeln?

Die Aufgabe gibt uns keine Reihenfolge vor. Ob wir zuerst eine 3 oder eine 5 würfeln, spielt keine Rolle.

Wonach suchen wir also? Entweder wir würfeln eine 3 und dann eine 5 oder wir würfeln eine 5 und dann eine 3.

Chance: 3 und dann eine 5:
Erster Wurf: Chance beträgt 1/6, dass es eine 3 wird
Zweiter Wurf: Chance beträgt 1/6, dass es eine 5 wird.
Insgesamt: 1/36

Chance: 5 und dann eine 3:
Erster Wurf: Chance beträgt 1/6, dass es eine 5 wird
Zweiter Wurf: Chance beträgt 1/6, dass es eine 3 wird.
Insgesamt: 1/36

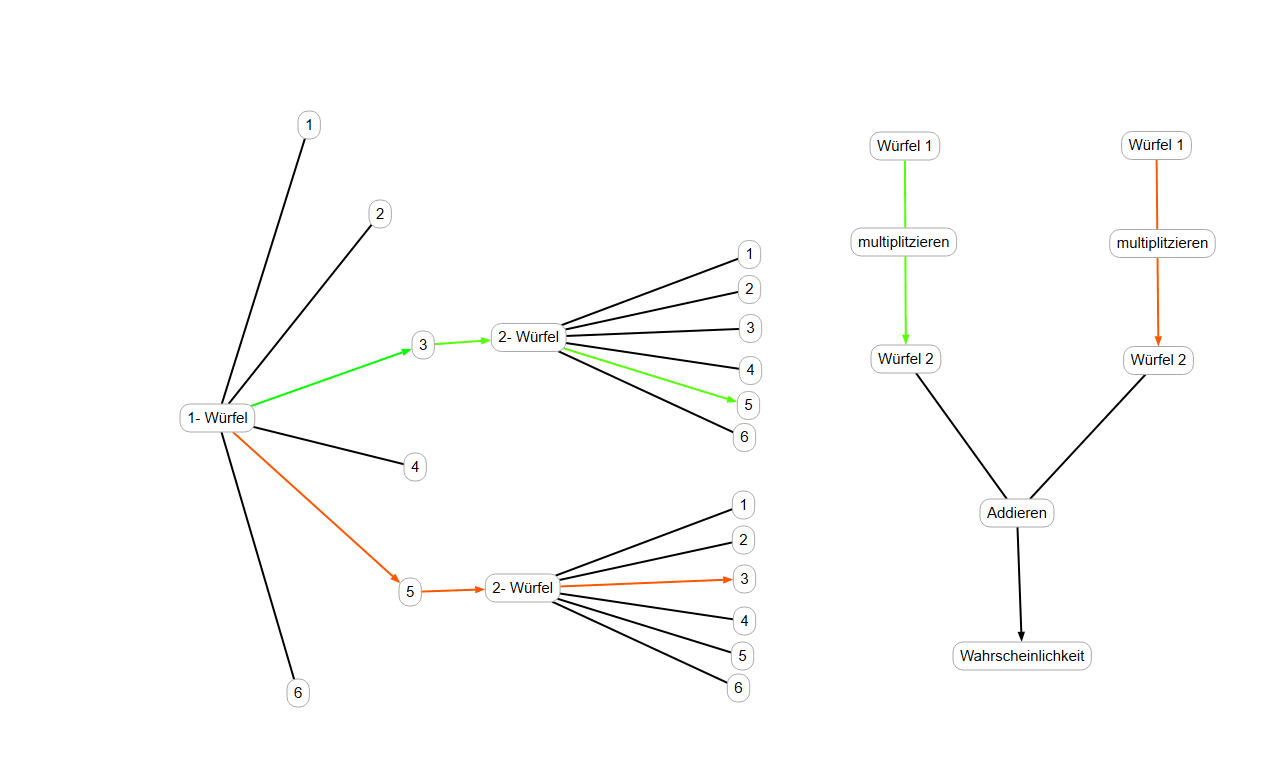
Es gibt also in unserem Stammbaum zwei Möglichkeiten von Links, nach Rechts zu gehen: 3:5 oder 5:3.

Diese zwei Linien werden miteinander addiert:

P (E) = 1/6 * 1/6 + 1/6 * 1/6
P (E) = 1/36 + 1/36
P (E) = 2/36

Zusammenfassung:

Der Stammbaum ist die beste Möglichkeit berechnen zu können, wie hoch die Wahrscheinlichkeit beim Würfeln ist. Dabei ist es sehr wichtig, die Aufgabe genau zu lesen. Gibt es eine feste Reihenfolge oder ist die Reihenfolge unerheblich?
Und dann muss man jeden Weg von Links nach Rechts nochmal addieren, falls dieser in Frage kommt.